- Original article
- Open access
- Published:
Holistic tactical-level planning in liner shipping: an exact optimization approach
Journal of Shipping and Trade volume 5, Article number: 8 (2020)
Abstract
Effective liner shipping is important for the global seaborne trade. The volume of cargoes transported by liner shipping has been increasing over the past decades. Liner shipping companies face three levels of decision problems, including strategic, tactical, and operational problems. The tactical-level decisions are commonly made every three to 6 months. These decisions include: (1) port service frequency determination; (2) fleet deployment; (3) sailing speed optimization; and (4) vessel schedule design. Most of the concurrent liner shipping studies have addressed the tactical-level decision problems separately. Even though a few studies have proposed joint planning models that capture multiple decision problems at the same time, none of the conducted studies has integrated all the four tactical-level decision problems. To address this gap in the state-of-the-art, this study presents a holistic optimization model that addresses all the tactical-level liner shipping decision problems, aiming to maximize the total profit obtained from liner shipping services. The key route service cost components, found in the liner shipping literature, are considered in this study, which include: (1) vessel operational cost; (2) vessel chartering cost; (3) port handling cost; (4) port late arrival cost; (5) fuel consumption cost; (6) container inventory costs in sea and at ports of call; and (7) emission costs in sea and at ports of call. An exact optimization approach is adopted for the developed mathematical model. The computational experiments, conducted for a set of Asia-North America liner shipping routes, showcase the efficiency of the proposed approach and offer some important managerial insights.
Background
Seaborne trade accounted for more than 80% of the total volume of the global merchandise trade in 2017 (UNCTAD, 2018). The global seaborne trade totaled to 10.7 billion tons of cargo that year. Moreover, it was forecasted to grow by 3.8% from 2018 to 2023. Since a significant portion of the global seaborne trade is carried by liner shipping, effective liner shipping is important for the global seaborne trade, and, thereby, for the overall supply chain management (Fugazza and Hoffmann, 2017; Hoffmann et al., 2017; Dulebenets, 2018a; Kavirathna et al., 2018; Achurra-Gonzalez et al., 2019). Liner shipping operates on fixed schedules along with fixed sequences of ports of call. The liner shipping industry is extremely competitive and capital intensive. Liner shipping companies face a number of challenges and are required to implement innovative ways to tackle these challenges. One of the most significant developments for the liner shipping industry was the introduction of containers in order to facilitate the movement of general consumption goods and high-valued cargoes. Container shipping is now the main focus of liner shipping, as it generated $7 billion in profits in the year of 2017 (UNCTAD, 2018). Still, there are some other important challenges, one of which is the improvement of the three key performance indicators, including operational efficiency, service effectiveness, and socio-economic impacts of liner shipping (Song et al., 2015). The improvement of these key performance indicators can be achieved by taking the appropriate actions at different levels of decision making in liner shipping.
Liner shipping companies tackle three levels of decision-making process, which are strategic, tactical, and operational decisions (Pesenti, 1995; Meng et al., 2014; Dulebenets et al., 2019). The scope of this study focuses on the tactical-level decision problems in liner shipping. The tactical-level decision problems, which are made three to 6 months in advance, include port service frequency determination, fleet deployment, sailing speed optimization, and vessel schedule design. In order to reduce the waiting time of containers at ports, a liner shipping company may increase port service frequencies. However, more frequent port visits would require deployment of a large number of vessels. Therefore, the liner shipping company will endure additional vessel operational costs. Moreover, while determining the port service frequency, the liner shipping company has to ensure that the container demand at ports and the profit margins are met. Several considerations are incorporated at the fleet deployment stage. The number of vessels in the liner shipping company’s fleet (i.e., fleet size) is generally limited. In order to meet the existing demand, the fleet size may not be sufficient. In such cases, the liner shipping company has to charter vessels from other liner shipping companies’ fleets, which incurs an additional cost (i.e., chartering cost). Moreover, based on the existing demand, the liner shipping company has to decide on the type of vessels (e.g., should the liner shipping company deploy mega-vessels that have large capacity or smaller vessels with lower capacity). Deployment of mega-vessels would result in economies of scale and would be suitable to meet high demand volumes. However, mega-vessels have high vessel operational costs and may cause some challenges for the marine container terminal operators, as they will be required to have a specific type of equipment in order to serve these mega-vessels.
Vessel sailing speed optimization is a crucial decision problem at the tactical level of liner shipping. Sailing speed bounds are generally dependent on the technical characteristics of vessel engines. A very low speed could deteriorate the vessel engines and shorten the lifespan of vessels. On the contrary, a high sailing speed would increase the fuel consumption cost. For instance, increasing the sailing speed by just 20% could increase the fuel consumption cost by up to 50% (Ronen, 2011). Such an increase in the fuel consumption cost may not be desirable, as the fuel consumption cost may account for about 75% of the total operational cost of vessels (Ronen, 2011). Over the recent years, a number of Emission Control Areas (ECAs) have been enforced by the International Maritime Organization (IMO) in order to reduce environmental pollution in those areas. Within the ECAs, vessels must use low-sulfur fuels, which are more expensive than the regular fuel. Such considerations should be also incorporated while selecting vessel sailing speeds. Among the tactical-level decision problems in liner shipping, the vessel schedule design (i.e., vessel scheduling) is the most intricate one (Meng et al., 2014; Dulebenets et al., 2019). Each vessel schedule contains the information regarding port arrival times, waiting times, handling times, departure times, etc. Moreover, each vessel schedule also has to incorporate some other important considerations, such as sailing speed, environmental sustainability issues, customer preferences, and others. The sailing speeds may be adjusted after the vessel schedules are published as long as the planned port arrival times are not violated.
All the aforementioned tactical-level decision problems are generally treated separately. Decisions, provided by separate solution approaches for separate decision problems, may not be compatible with each other (e.g., the required number of vessels, determined at the fleet deployment stage, may not be sufficient when solving the vessel scheduling problem, which will further result in violation of the target port service frequency). Also, an integrated methodology, which could simultaneously address all the four tactical-level decision problems, will be able to effectively assist liner shipping companies with decision making and meet certain profit margins. However, to the authors’ knowledge, no prior studies have combined all the tactical-level decision problems to provide an integrated solution approach. The latter can be explained by the fact that the mathematical formulation that incorporates all the four tactical-level decision problems in liner shipping will have significantly more decision and auxiliary variables, which will increase its computational complexity and impose potential challenges in selection of the appropriate solution approach.
Acknowledging this gap in the state-of-the-art, the present study formulates a novel holistic mathematical model that incorporates all the decision problems at the tactical level of liner shipping. The remainder of this manuscript is structured as follows. Section 2 provides a concise review of the tactical-level liner shipping studies, which are related to the theme of this study. In section 3, the problem environment is formally described in detail. The formulation of the proposed model is outlined in section 4. Section 5 presents the computational experiments that were conducted to validate the proposed approach and obtain some managerial insights. Finally, this study is concluded in section 6.
Review of the relevant studies
This section of the manuscript highlights findings from the literature review regarding the decision problems at the tactical level of liner shipping. Furthermore, contributions of this study to the state-of-the-art are explicitly outlined in this section as well.
Service frequency determination
A number of liner shipping studies have integrated port service frequency determination with other decision problems. For example, Bendall and Stent (2001) studied a joint fleet deployment and fleet size design along with port service frequency determination. Hsu and Hsieh (2007) presented a methodology that can be used to determine port service frequency and vessel size for a maritime hub-and-spoke container shipping network. Meng and Wang (2011) specifically focused on planning shipping operations for a long-haul liner shipping port rotation, aiming to determine fleet deployment plan, port service frequency, and vessel sailing speed. Weekly and bi-weekly port service frequencies are considered as the most common ones in the liner shipping industry (Meng et al., 2014; Dulebenets et al., 2019). On the other hand, Lin and Tsai (2014) and Zhang and Lam (2014) discussed various aspects of daily service frequency and its impacts on the overall efficiency of liner shipping operations. In contrast to common liner shipping scheduling models that assume the fixed port service frequency, Giovannini and Psaraftis (2019) presented a new model, aiming to identify potential impacts of the variable port service frequency, while addressing vessel scheduling decisions. The computational experiments, which were conducted as a part of that study, demonstrated that the variable port service frequency was more promising as compared to the fixed port service frequency in terms of the total profit generated.
Fleet deployment
A significant portion of the fleet deployment studies tackled additional decision problems, such as vessel routing, network design, empty container repositioning, etc. (Álvarez, 2009; Gelareh and Pisinger, 2011; Gelareh et al., 2013; Huang et al., 2015; Wang et al., 2018a; Zhen et al., 2019a,b). Álvarez (2009) aimed to design optimal routes for container vessels and determine the required number of vessels as well as the vessel type. Gelareh and Pisinger (2011) and Gelareh et al. (2013) presented optimization models for an integrated liner shipping network design and fleet deployment problem. Huang et al. (2015) noted that container demand was subject to seasonality and fluctuated every three to 6 months. Based on the latter feature, the study proposed a mixed-integer programming model to modify the existing liner shipping networks, re-deploy vessels, and determine the appropriate cargo routes. Ng (2015) presented a fleet deployment model, where the container demand was stochastic. Zhao et al. (2016) aimed to deploy vessels based on a route risk evaluation model, which considered several environmental factors that could disrupt safety of navigation. The developed model was solved using the firefly algorithm. Ng and Lin (2018) approximated lower and upper bounds on the optimal shipping cost using a fleet deployment model, where only the conditional demand information was available. Wang et al. (2018a) presented a vessel chartering model, which integrated fleet composition and sailing speed optimization. Zhen et al. (2019a) modeled a demand fulfillment and fleet deployment problem, where the container overload risk was accounted for. On the other hand, Zhen et al. (2019b) developed an integrated fleet deployment, vessel scheduling, and container routing model for liner shipping.
Sailing speed optimization
The sailing speed optimization studies primarily focus on modeling fuel consumption, since vessel sailing speed is a major predictor of fuel consumption by the main vessel engines (Fagerholt et al., 2010; Ronen, 2011; Cheaitou and Cariou, 2012; Yao et al., 2012; Sheng et al., 2015; Wang and Meng, 2015; Wong et al., 2015; Tan et al., 2018). Fagerholt et al. (2010) highlighted that fuel consumption could be estimated as a cubic function of vessel sailing speed. Cheaitou and Cariou (2012) proposed a sailing speed optimization model, where the transported perishable goods were sensitive to the transit time, while the transported dry and frozen goods were not sensitive to the transit time. Throughout the sailing speed optimization, Wang and Meng (2012a) considered transshipment and routing of containers. Yao et al. (2012) proposed a fuel management scheme, which included three major components: (1) selection of fueling ports; (2) estimation of fueling amount; and (3) adjustment of sailing speeds. Sheng et al. (2015) presented a sailing speed optimization and refueling model, which considered uncertainties in fuel price and fuel consumption. Wang and Meng (2015) focused on a sailing speed optimization and refueling problem in a liner shipping network, considering potential differences between the planned vessel speed and the real vessel speed. Wong et al. (2015) aimed to reduce fuel consumption as well as carbon emissions through slow steaming. Wang and Wang (2016) studied the vessel sailing speed optimization problem, where the liner shipping company had to allocate a limited number of vessels between different routes. Tan et al. (2018) proposed a mathematical model to jointly optimize sailing speeds and vessel schedules, taking into account the dam transit time uncertainty. Wang et al. (2018b) presented a vessel sailing speed optimization model, where the unit fuel cost was stochastic but did not follow any particular distribution. Cheaitou and Cariou (2019) considered an elastic container demand, which was dependent on the vessel sailing speed.
Vessel schedule design
Vessel schedule design is the most convoluted tactical-level decision problem in liner shipping. A number of researchers have concentrated on the basic vessel scheduling decisions, which include sailing speed at each voyage leg, arrival time, waiting time, handling time, and departure time at each port of call (Chen et al., 2007; Zhen et al., 2016; Dulebenets and Ozguven, 2017; Dulebenets, 2018b; Wang et al., 2019). Zhen et al. (2016) estimated arrival times and dwell times at ports of call, including transshipment hubs. Wang et al. (2019) developed a tailored branch-and-cut algorithm to solve a mixed-integer programming model that aimed to facilitate intercontinental liner shipping. The objective function of the presented mathematical model maximized the total service profit. Various sources of uncertainty in liner shipping that can potentially influence vessel schedules, such as uncertainties in shipment demand, port times, sailing times, etc., have been modeled by a number of studies (Wang and Meng, 2012b,c; Aydin et al., 2017; Tan et al., 2018; Gürel and Shadmand, 2019). For example, Wang and Meng (2012b) addressed uncertainties in both waiting and handling times at ports of call throughout vessel scheduling. On the other hand, Gürel and Shadmand (2019) modeled uncertainties in port waiting and handling times, capturing a heterogeneous nature of the vessel fleet.
A few studies have proposed collaborative agreements between liner shipping companies and marine container terminal (MCT) operators in order to benefit from multiple port arrival time windows (TWs) as well as the associated handling rates (HRs) (Alharbi et al., 2015; Wang et al., 2014; Liu et al., 2016; Dulebenets, 2019). Alharbi et al. (2015) formulated a mathematical model, aiming to assist liner shipping companies with selection of the optimal port arrival TW from the available TWs at a given port of the liner shipping route. Dulebenets (2019) proposed a collaborative agreement between MCT operators and liner shipping companies, where at each port a given liner shipping company could select from multiple TWs and multiple HRs, which had different handling costs. Furthermore, some of the concurrent vessel scheduling studies have considered the impact of liner shipping on the environment, such as emissions of harmful substances (Fagerholt and Psaraftis, 2015; De et al., 2016; Dulebenets, 2018c,d; Giovannini and Psaraftis, 2019; Cheaitou and Cariou, 2019). For example, Fagerholt and Psaraftis (2015) investigated the use of low-sulfur fuel, which is more expensive as compared to the regular fuel, within ECAs. De et al. (2016) examined various strategies, such as slow steaming and speed optimization, in order to reduce carbon dioxide emissions.
Existing state-of-the-art gaps and contributions of this study
From a detailed review of the studies on tactical-level decisions in liner shipping, it was revealed that some of the studies incorporated multiple tactical-level decision problems; however, none of them addressed all the four decision problems simultaneously. Decisions, provided by separate solution approaches for separate decision problems, may not be compatible with each other. Also, an integrated methodology, which could simultaneously address all the four tactical-level decision problems, will be able to effectively assist liner shipping companies with decision making and meet certain profit margins. Acknowledging this gap in the state-of-the-art, this study makes the following contributions:
A novel holistic optimization model for the tactical-level decisions in liner shipping is proposed, which captures all the tactical-level decision problems, including port service frequency determination, fleet deployment, sailing speed optimization, and vessel schedule design.
Different types of vessels can be assigned to different liner shipping routes by the developed model.
Unlike the majority of the previously conducted liner shipping studies, which assume that the fuel consumption is solely determined based on the vessel sailing speed, this study directly accounts for both vessel sailing speed and vessel payload in the estimation of the fuel consumption.
Under the proposed mathematical model, the container demand at ports is elastic and dependent on the vessel sailing speed at each voyage leg, which is in line with real-life liner shipping operations (i.e., container demand generally decreases with increasing transit time of containers).
In contrast to a significant portion of the concurrent liner shipping literature, multiple TWs and HRs are offered to serve the vessels at each port of call in order to improve the efficiency of liner shipping operations, reduce the total route service cost, and improve the utilization of the available MCT handling equipment.
In contrast to most of the existing liner shipping literature, container inventory costs both in sea and at ports are captured by the developed mathematical model.
In order to enhance the environmental sustainability of the international trade and liner shipping operations, the proposed mathematical model captures the quantity of emissions that are produced by vessels in sea and from container handling at ports.
Problem description
This section presents a detailed description of the problem, which is addressed in this study, including the following aspects: (1) liner shipping route description; (2) fleet deployment; (3) service of vessels at ports; (4) fuel consumption; (5) container demand sensitivity; (6) port service frequency; (7) container inventory; (8) modeling emissions; and (9) objective of the liner shipping company. Note that all the major tactical-level decisions, which have to be addressed by a given liner shipping company, are captured throughout this study.
Liner shipping route description
Each liner shipping route is generally served either by an individual liner shipping company or a set of different liner shipping companies (or alliances). The routes consist of multiple ports of call. The number of ports to be called by vessels may vary from one liner shipping route to another. Let R = {1, …, n1} denote the set of port rotations (i.e., the order of ports to be called), while the set of ports to be visited at port rotation r will be further referred to as \( {P}_r=\left\{1,\dots, {n}_r^2\right\},r\in R \). Two consecutive ports p and p + 1 are connected via voyage leg p. Each liner shipping company generally provides details about the port rotations that are currently served by the company, including the following information: (1) names of ports of call; (2) countries of the ports; (3) distance to the subsequent port to be visited; and others. Each port of call under every port rotation has fixed vessel schedules (e.g., arrival times, handling times, departure times).
A liner shipping network with four port rotations is illustrated in Fig. 1. The itinerary of each port rotation forms a loop – i.e., each port rotation starts and ends at the same port. For instance, in port rotation “1”, vessels start their voyage at Tokyo, then stop at Nagoya, Yokkaichi, Kobe, and return to Tokyo. The number of ports of call for port rotation “1” is 4 (i.e., \( {n}_1^2 \) = 4). Note that a given port can be included in multiple port rotations. Hong Kong, for example, is included in port rotations “2” and “3”. Furthermore, a given port can be visited more than once in a single port rotation. Based on the provided example, Penang is called twice in port rotation “4”. These calls can be distinguished by referring to the port calling sequence.
Fleet deployment
At the fleet deployment stage, the liner shipping company assigns the available vessel types for service of the port rotations. Let V = {1, …, n3} be the set of vessel types to be used by the liner shipping company to serve the port rotations. Let dvr = 1 if vessel type v is assigned to serve port rotation r. Generally, liner shipping companies assign one vessel type for service of each port rotation (Wang and Meng, 2017). The latter condition can be enforced using the following relationship:
A vessel string of the selected vessel type to be assigned for service of a given port rotation is assumed to be homogeneous (i.e., vessels of the same type are assumed to have the same technical properties, including the maximum sailing speed, fuel consumption rate, emissions produced by the main and auxiliary vessel engines, and others). Although such an assumption may not be applicable in some instances (e.g., technical properties for vessels of the same type may vary due to differences in age, vessel structure, capacity, past maintenance/repairs, and other reasons), it is commonly used at the fleet deployment and vessel scheduling stages in the liner shipping literature and in practice as well (Wang and Meng, 2017). If the required number of vessels of a specific type to be deployed for service of a given port rotation exceeds the total number of available vessels of that type (\( {q}_v^{own-m},v\in V \) – vessels), which are owned by the liner shipping company, a given liner shipping company may charter vessels from the other liner shipping companies. In such case, the liner shipping company incurs an additional cost (\( {c}_v^{char},v\in V \) – USD/day) for chartering vessels.
Service of vessels at ports
Certain arrival TWs are offered for the vessels by an MCT operator at each port of a given port rotation. Let \( {T}_{rp}=\left\{1,\dots, {n}_{rp}^4\right\},r\in R,p\in {P}_r \) be the set of available arrival TWs at port p of port rotation r. Two attributes are associated with each TW, offered at a given port, including the following: (1) \( {\tau}_{rp t}^{st},r\in R,p\in {P}_r,t\in {T}_{rp} \) – start of TW t at port p of port rotation r (hours); and (2) \( {\tau}_{rp t}^{end},r\in R,p\in {P}_r,t\in {T}_{rp} \) – end of TW t at port p of port rotation r (hours). The arrival TW is negotiated between the liner shipping company and each MCT operator. In certain cases, only one arrival TW can be offered to the liner shipping company at a given port (e.g., busy ports with frequent vessel arrivals). Vessels are expected to arrive within the agreed TW at each port. Similar to Fagerholt (2001), this study assumes that the arrival TWs at ports of call are “soft” (i.e., vessels are permitted to arrive before the TW starts and after the TW ends). In case of an early arrival, a vessel is expected to wait for service in the dedicated area of the port. In case of a late arrival, service of a vessel is expected to start upon its arrival; however, the MCT operator will impose a late arrival cost to the liner shipping company, which is proportional to the total late arrival hours (\( {\boldsymbol{\tau}}_{rp}^{late},r\in R,p\in {P}_r \) – hours) and the unit late arrival cost (\( {c}_{rp}^{late},r\in R,p\in {P}_r \) – USD/hour). The late arrival cost is imposed to the liner shipping company due to the fact that vessel arrival delays may significantly disrupt the port operations (e.g., cause congestion at a given port). The total late arrival cost (LAC – USD) can be estimated based on the following relationship:
Each MCT operator is assumed to offer different HRs to the liner shipping company for service of the arriving vessels. Let \( {H}_{rp t}=\left\{1,\dots, {n}_{rp t}^5\right\},r\in R,p\in {P}_r,t\in {T}_{rp} \) be the set of HRs at port p of port rotation r available during TW t. The handling productivity, associated with a given HR, determines the number of twenty-foot equivalent units (TEUs) to be handled at each vessel per hour and will be referred to as phrpthv, r ∈ R, p ∈ Pr, t ∈ Trp, h ∈ Hrpt, v ∈ V (TEUs/hour). In certain cases, only one HR can be offered to the liner shipping company at a given port (e.g., the MCT operator may have to allocate the handling equipment for service of the other vessels during high-demand periods). If \( {\boldsymbol{QC}}_{rp}^{PORT},r\in R,p\in {P}_r \) (TEUs) is the quantity of containers to be handled at port p of port rotation r, the handling time for vessels of type v at port p of port rotation r during TW t under HR h will be \( {\boldsymbol{\tau}}_{rp t hv}^{hand}=\frac{{\boldsymbol{QC}}_{rp}^{PORT}}{ph_{rp t hv}}\forall r\in R,p\in {P}_r,t\in {T}_{rp},h\in {H}_{rp t},v\in V \) (hours). The handling productivity and the corresponding handling cost (\( {c}_{rp t hv}^{hand},r\in R,p\in {P}_r,t\in {T}_{rp},h\in {H}_{rp t},v\in V \) – USD/TEU) are negotiated between the liner shipping company and the MCT operator at each port of a given port rotation. Let xrpthv = 1 if HR h is selected for service of type v vessels at port p of port rotation r during TW t; then, the total port handling cost (PHC – USD) can be estimated based on the following relationship:
Fuel consumption
As previously discussed, the liner shipping company deploys a homogenous vessel fleet at each port rotation. The fuel consumption rate of the main vessel engines, which turn vessel propellers, is expected to be the same for homogenous vessels (Wang and Meng, 2017). Note that the fuel consumption rate is influenced by a number of different factors, including weather conditions, payload, sailing speed, and vessel geometric characteristics (Wang and Meng, 2012a; Kontovas, 2014). However, the vessel sailing speed was found to be the major factor influencing the fuel consumption (Wang and Meng, 2012a). The design fuel consumption per nautical mile (nmi) for vessels of type v at voyage leg p of port rotation r (\( {\boldsymbol{f}}_{rpv}^{design},r\in R,p\in {P}_r,v\in V \) – tons/nmi) can be estimated based on the following relationship (Wang and Meng, 2012a):
where:
αv, γv, v ∈ V – are the coefficients of the fuel consumption function for vessel type v;
ϑrp, r ∈ R, p ∈ Pr – is the vessel sailing speed at voyage leg p of port rotation r (knots).
Some of the liner shipping studies have highlighted that payload of vessels is one of the major predictors of fuel consumption by vessel engines (Psaraftis and Kontovas, 2013; Kontovas, 2014). Assuming that the design fuel consumption is based on the maximum payload capacity, the fuel consumption of vessels (frpv, r ∈ R, p ∈ Pr, v ∈ V – tons/nmi) can be estimated from the following relationship (MAN Diesel & Turbo, 2012; Kontovas, 2014; Adland and Jia, 2016):
where:
\( {\boldsymbol{QC}}_{rp}^{SEA},r\in R,p\in {P}_r \) – is the quantity of containers to be transported at voyage leg p of port rotation r (TEUs);
AWC – is the average weight of cargo inside a standard 20-ft container (tons);
LWTv, v ∈ V – is the empty weight of a vessel of type v (tons);
TWCv, v ∈ V – is the total weight of containers that can be loaded on a vessel of type v (tons).
The total vessel fuel consumption cost (FCC – USD) can be estimated based on the total fuel consumption, the unit fuel cost (cfuel – USD/ton), and the voyage leg length (lrp, r ∈ R, p ∈ Pr – nmi) using the following relationship:
Note that the fuel consumption of the auxiliary vessel engines (that are commonly used to provide power on board the vessels) does not significantly fluctuate throughout the vessel voyage at a given port rotation and is accounted for in the vessel operational cost. Once a sailing speed is selected for a given voyage leg, it is assumed to remain the same while the vessel is sailing at that voyage leg. This study does not account for the factors that may result in fluctuations of the vessel sailing speed along a given voyage leg (e.g., wind speed, adverse weather conditions, height of waves, main engine malfunctioning, errors of the crew).
Several factors influence the vessel sailing speed choice. The highest possible sailing speed is selected according to the capacity of the main vessel engines (Psaraftis and Kontovas, 2013). The lowest sailing speed, on the other hand, is typically selected to decrease potential wear of the main vessel engines (Wang et al., 2013). Decreasing the vessel sailing speed will lead to reduction in the fuel consumption, and, thereby, the fuel consumption cost as well as the amount of emissions that are produced in sea. However, reducing the sailing speed will further cause an increase in the total transit time of containers along with the associated inventory costs. The latter will cause an increase in the total turnaround time of vessels, which will further necessitate the liner shipping company to deploy more vessels in order to guarantee a certain port service frequency. If more vessels are deployed, the total vessel operational/chartering cost will become higher. The total vessel turnaround time can be decreased by requesting HRs with higher handling productivities at ports of call. However, the latter will lead to increasing port handling cost at each port rotation and increasing amount of emissions from the handling equipment. Therefore, vessel sailing speeds at each port rotation should be selected by considering all the aforementioned factors and associated tradeoffs. The sailing time at voyage leg p of port rotation r (\( {\boldsymbol{\tau}}_{rp}^{sail},r\in R,p\in {P}_r \) – hours) can be estimated based on the voyage leg length and the vessel sailing speed using the following relationship:
Container demand sensitivity
Inspired by Cheaitou and Cariou (2019), this study considers the container demand at ports (\( {\boldsymbol{QC}}_{rp}^{PORT},r\in R,p\in {P}_r \) – TEUs) to be elastic and sensitive to the vessel sailing speed. Generally, customers transport a larger amount of cargo if the vessel sailing speed at a voyage leg is higher. Thus, the relationship between the container demand at ports and the vessel sailing speed can be expressed by the following equation (Cheaitou and Cariou, 2019):
where:
\( {\alpha}_{rp}^{dem},{\beta}_{rp}^{dem},r\in R,p\in {P}_r \) – are the coefficients of the container demand sensitivity to the vessel sailing speed at port p of port rotation r.
Upon arrival at a port of call, the import containers of the respective port (from the perspective of the MCT operator) will be unloaded from the vessels, and the export containers of the respective port will be loaded on board the vessels. Therefore, the quantity of containers to be transported at the voyage legs (\( {\boldsymbol{QC}}_{rp}^{SEA},r\in R,p\in {P}_r \) – TEUs) can be determined from the following relationships:
where:
Importrp, r ∈ R, p ∈ Pr – is the portion of import containers at port p of port rotation r;
\( {QC}_r^{SEA-0},r\in R \) – is the total quantity of containers on board the vessel before it is moored at the first port of call (i.e., port “1”) under port rotation r (TEUs).
Note that the quantity of containers on board a given vessel must not exceed the total cargo carrying capacity of that vessel type. Hence, the following relationship must be maintained:
where:
M – is a large positive number.
Port service frequency
Generally, the port service frequency is established based on the existing demand at each port of a given port rotation. In order to guarantee the agreed port service frequency at each port rotation, the liner shipping company has to assure that the following relationship will be maintained (Wang et al., 2014; Alharbi et al., 2015; Dulebenets and Ozguven, 2017):
where:
qr, r ∈ R – is the total number of vessels that will be deployed for service of port rotation r (vessels);
ϕr, r ∈ R – is the port service frequency for port rotation r (days);
24 – is the total number of hours in a day (hours/day)
\( {\boldsymbol{\tau}}_{rp}^{wait},r\in R,p\in {P}_r \) – is the vessel waiting time at port p of port rotation r (hours).
The right-hand side of equality (12) represents the total vessel turnaround time at port rotation r (i.e., the total time required by the vessels, which were allocated for that port rotation, to visit all the ports of call and return to the first port of call). The vessel turnaround time at each port rotation is composed of the following components: (i) total vessel sailing time over all the voyage legs of a given port rotation; (ii) total port handling time over all the ports of a given port rotation; and (iii) total port waiting time over all the ports of a given port rotation. The required number of vessels to be deployed for service of a given port rotation can be further determined by dividing the total turnaround time by the port service frequency and the integer “24” (which denotes the total number of hours in a day). As previously discussed, the vessels, used for service of a given port rotation, can be owned by the liner shipping company and/or chartered from other liner shipping companies. It is assumed that the vessels, deployed for a given port rotation, are homogeneous and have the same unit vessel operational cost (\( {c}_v^{oper},v\in V \) – USD/day). The total vessel operational cost (VOC – USD) and the total number of vessels that will deployed for service of port rotation r (qr, r ∈ R – vessels) can be estimated based on the following relationships:
where:
\( {\boldsymbol{q}}_{rv}^{own},r\in R,v\in V \) – is the total number of vessels of type v, owned by the liner shipping company, that will be deployed for service of port rotation r (vessels);
\( {\boldsymbol{q}}_{rv}^{char},r\in R,v\in V \) – is the total number of vessels of type v, chartered by the liner shipping company, that will be deployed for service of port rotation r (vessels).
The total vessel chartering cost (VCC – USD) can be estimated based on the unit chartering cost (\( {c}_v^{char},v\in V \) – USD/day), the number of chartered vessels, and the established port service frequency using the following relationship:
Container inventory
Two types of inventory costs are considered in this study: (i) inventory cost in sea; and (ii) inventory cost at ports of call. The inventory cost in sea is proportional to the total transit time of containers, transported between consecutive ports of call. Similarly, the inventory cost at ports is proportional to the total waiting time and the total handling time of containers at ports. Generally, sailing time of vessels in sea is larger as compared to waiting and handling times of vessels at ports; therefore, the inventory cost in sea is expected to be larger than the inventory cost at ports of call. The total container inventory costs in sea and at ports of call (denoted as CICSEA – USD and CICPORT – USD, respectively) can be estimated based on the following relationships (Wang et al., 2014; Dulebenets, 2018a):
where:
cinv – is the unit inventory cost (USD/TEU/hour).
Modeling emissions
In order to improve the environmental sustainability of container shipping, the liner shipping company has to account for the emissions (e.g., CO2, SOx, NOx, etc.), produced in sea and at ports of call throughout container handling. The amount of emissions produced at voyage leg p of port rotation r (\( {\boldsymbol{EP}}_{rp}^{SEA},r\in R,p\in {P}_r \) – tons) can be determined based on the fuel consumption and the emission factor in sea (EFSEA – tons of emissions/ton of fuel) using the following relationship (Psaraftis and Kontovas, 2013; Kontovas, 2014; Dulebenets, 2018a):
The amount of emissions produced at ports is dependent on the type of equipment used by the MCT operators. Handling productivity is also a major factor influencing the amount of emissions produced. If an HR with a high handling productivity is requested by the liner shipping company at a given port of call, more equipment will be required for container handling operations, which will increase the amount of emissions produced. The amount of emissions produced at port p of port rotation r (\( {\boldsymbol{EP}}_{rp}^{PORT},r\in R,p\in {P}_r \) – tons) can be determined based on the quantity of containers to be handled at the port, the emission factor at the port (\( {EF}_{rphv}^{PORT},r\in R,p\in {P}_r,h\in {H}_{rpt},v\in V \) – tons of emissions/TEU), and the selected HR using the following relationship (Tran et al., 2017; Dulebenets, 2018c):
The total emission cost in sea (ECSEA – USD) and the total emission cost at ports of call (ECPORT – USD) can be calculated based on the total amount of emissions, produced in sea as well as at ports of call, and the unit emission cost (cemis – USD/ton) using the following relationships:
Note that eqs. (18)–(21) can be applied for modeling the major pollutants, produced by vessels in sea and by the container handling equipment at ports.
Objective of the liner shipping company
This study assumes that the objective of the liner shipping company is to maximize the total profit. Such an assumption is in line with the previously conducted liner shipping studies (Giovannini and Psaraftis, 2019; Dulebenets et al., 2019). The total profit can be calculated as a difference between the total revenue and the total route service cost. The total revenue (REV – USD) can be estimated based on the quantity of containers to be delivered to ports of call at the considered port rotations and the unit freight rate (\( {c}_{rp}^{rev},r\in R,p\in {P}_r \) – USD/TEU) using the following relationship (Giovannini and Psaraftis, 2019):
As for the total route service cost, the key route service cost components, found in the liner shipping literature, are considered in this study, which include: (1) vessel operational cost; (2) vessel chartering cost; (3) port handling cost; (4) port late arrival cost; (5) fuel consumption cost; (6) container inventory costs in sea and at ports of call; and (7) emission costs in sea and at ports of call. In order to maximize the total profit, the following major decisions have to be taken into consideration by the liner shipping company: (1) the number of vessels of each type, owned by the liner shipping company, that will be deployed for each port rotation; (2) the number of vessels of each type, chartered by the liner shipping company, that will be deployed for each port rotation; (3) port service frequency at each port rotation; (4) the sailing speed at each voyage leg of each port rotation; (5) the arrival TW at each port of call for each port rotation; and (6) the HR at each port of call for each port rotation.
Holistic mathematical model
This section of the manuscript provides a detailed description of the Holistic Optimization Model for Tactical-Level Planning in Liner Shipping (HOMTLP).
Preliminary linearization techniques
Constraint sets (4), (7), and (8) are generally used in the liner shipping literature for estimating the design fuel consumption, the vessel sailing time at voyage legs of the liner shipping route for each port rotation, and the container demand at ports, respectively (Wang et al., 2013; Wang et al., 2014; Alharbi et al., 2015; Cheaitou and Cariou, 2019). However, these constraint sets are nonlinear. In order to reduce the computational complexity of the proposed mathematical model, a number of commonly used linearization techniques will be further applied. In particular, the vessel sailing speed (ϑrp, r ∈ R, p ∈ Pr – knots) will be replaced with its reciprocal \( {\boldsymbol{y}}_{rp}=\frac{1}{{\boldsymbol{\vartheta}}_{rp}}\forall r\in R,p\in {P}_r \) (knots− 1) in order to linearize constraint sets (7) and (8). Furthermore, the design fuel consumption function \( {\boldsymbol{f}}_{rpv}^{design},r\in R,p\in {P}_r,v\in V \) can be linearized using its piecewise linear approximation. Denote \( {S}_v=\left\{1,\dots, {n}_v^6\right\},v\in V \) as the set of linear segments in the piecewise function for the design fuel consumption. The design fuel consumption will be estimated for each one of the segments, which will allow overcoming nonlinearity of constraint set (4). Although the aforementioned linearization strategies will not linearize the whole mathematical model (as the model includes some other nonlinear variables), they will allow reducing the degree of the model’s nonlinearity. The latter is also expected to reduce the computational complexity of the proposed mathematical model.
Figure 2 presents an illustrative example of a linear approximation for the design fuel consumption function \( {\boldsymbol{f}}^{design}=\frac{\gamma {\left(\boldsymbol{\vartheta} \right)}^{\left(\alpha -1\right)}}{24} \). In this example, the values of α and γ were set to 3 and 0.012, respectively (Wang and Meng, 2012a; Psaraftis and Kontovas, 2013). The sailing speed reciprocal was allowed to vary between 0.040 knots−1 and 0.067 knots−1 (i.e., 15 ≤ ϑ ≤ 25) (Wang and Meng, 2012a,b). After introducing 10 linear segments, it can be observed that the linear approximation for the design fuel consumption function aligns very closely with the original nonlinear design fuel consumption function.
Nomenclature
Sets | |
|---|---|
R = {1, …, n1} | set of port rotations (port rotations) |
\( {P}_r=\left\{1,\dots, {n}_r^2\right\},r\in R \) | set of ports under port rotation r (ports) |
V = {1, …, n3} | set of available vessel types (vessel types) |
\( {T}_{rp}=\left\{1,\dots, {n}_{rp}^4\right\},r\in R,p\in {P}_r \) | set of available TWs at port p of port rotation r (TWs) |
\( {H}_{rpt}=\left\{1,\dots, {n}_{rpt}^5\right\},r\in R,p\in {P}_r, \) t ∈ Trp | set of available HRs at port p of port rotation r during TW t (HRs) |
\( {S}_v=\left\{1,\dots, {n}_v^6\right\},v\in V \) | set of linear segments in the piecewise function of the design fuel consumption for vessel type v (segments) |
Decision Variables | |
yrp ∈ ℝ+ ∀ r ∈ R, p ∈ Pr | vessel sailing speed reciprocal at voyage leg p of port rotation r (knots−1) |
ϕr ∈ ℕ ∀ r ∈ R | port service frequency for port rotation r (days) |
\( {\boldsymbol{q}}_{rv}^{own}\in \mathbb{N}\forall r\in R,v\in V \) | number of vessels of type v in company’s own fleet for deployment at port rotation r (vessels) |
\( {\boldsymbol{q}}_{rv}^{char}\in \mathbb{N}\forall r\in R,v\in V \) | number of chartered vessels of type v for deployment at port rotation r (vessels) |
\( {\boldsymbol{d}}_{rv}\in \mathbbm{B}\forall r\in R,v\in V \) | =1 if vessel type v is assigned to serve port rotation r (=0 otherwise) |
\( {\boldsymbol{z}}_{rp t}\in \mathbbm{B}\forall r\in R,p\in {P}_r,t\in {T}_{rp} \) | =1 if TW t is selected at port p of port rotation r (=0 otherwise) |
\( {\boldsymbol{x}}_{rp thv}\in \mathbbm{B}\forall r\in R,p\in {P}_r,t\in {T}_{rp}, \) h ∈ Hrpt, v ∈ V | =1 if HR h is selected for vessels of type v at port p of port rotation r during TW t (=0 otherwise) |
\( {\boldsymbol{g}}_{rpvs}\in \mathbbm{B}\forall r\in R,p\in {P}_r,v\in V,s\in {S}_v \) | =1 if segment s is selected to estimate the fuel consumption of vessel type v at voyage leg p of port rotation r (=0 otherwise) |
Auxiliary Variables | |
qr ∈ ℕ ∀ r ∈ R | number of vessels that will be deployed at port rotation r (vessels) |
RFrpvs ∈ ℝ+ ∀ r ∈ R, p ∈ Pr, v ∈ V, s ∈ Sv | fuel consumption under segment s for vessel type v at voyage leg p of port rotation r (tons/nmi) |
\( {\boldsymbol{QC}}_{rp}^{SEA}\in \mathbb{N}\forall r\in R,p\in {P}_r \) | quantity of containers to be transported at voyage leg p of port rotation r (TEUs) |
\( {\boldsymbol{QC}}_{rp}^{PORT}\in \mathbb{N}\forall r\in R,p\in {P}_r \) | quantity of containers to be handled at port p of port rotation r (TEUs) |
\( {\boldsymbol{\tau}}_{rp}^{sail}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | sailing time at voyage leg p of port rotation r (hours) |
\( {\boldsymbol{\tau}}_{rp}^{arr}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | arrival time at port p of port rotation r (hours) |
\( {\boldsymbol{\tau}}_{rp}^{wait}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | waiting time of a vessel at port p of port rotation r (hours) |
\( {\boldsymbol{\tau}}_{rp}^{late}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | vessel late arrival at port p of port rotation r (hours) |
\( {\boldsymbol{\tau}}_{rp thv}^{hand}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r,t\in {T}_{rp}, \) h ∈ Hrpt, v ∈ V | handling time for type v vessels at port p of port rotation r during TW t under HR h (hours) |
\( {\boldsymbol{\tau}}_{rp}^{dep}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | departure time from port p of port rotation r (hours) |
\( {\boldsymbol{EP}}_{rp}^{SEA}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | amount of emissions produced at voyage leg p of port rotation r (tons) |
\( {\boldsymbol{EP}}_{rp}^{PORT}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | amount of emissions produced at port p of port rotation r (tons) |
REV ∈ ℝ+ | total revenue (USD) |
VOC ∈ ℝ+ | total vessel operational cost (USD) |
VCC ∈ ℝ+ | total vessel chartering cost (USD) |
PHC ∈ ℝ+ | total port handling cost (USD) |
LAC ∈ ℝ+ | total late arrival cost (USD) |
FCC ∈ ℝ+ | total fuel consumption cost (USD) |
CICSEA ∈ ℝ+ | total container inventory cost in sea (USD) |
CICPORT ∈ ℝ+ | total container inventory cost at ports of call (USD) |
ECSEA ∈ ℝ+ | total emission cost in sea (USD) |
ECPORT ∈ ℝ+ | total emission cost at ports of call (USD) |
Parameters | |
n1 ∈ ℕ | number of port rotations (port rotations) |
\( {n}_r^2\in \mathbb{N}\forall r\in R \) | number of ports under port rotation r (ports) |
n3 ∈ ℕ | number of available vessel types (vessel types) |
\( {n}_{rp}^4\in \mathbb{N}\forall r\in R,p\in {P}_r \) | number of available TWs at port p of port rotation r (TWs) |
\( {n}_{rp t}^5\in \mathbb{N}\forall r\in R,p\in {P}_r,t\in {T}_{rp} \) | number of available HRs at port p of port rotation r during TW t (HRs) |
\( {n}_v^6\in \mathbb{N}\forall v\in V \) | number of segments in the design fuel consumption function for vessel type v (segments) |
lrp ∈ ℝ+ ∀ r ∈ R, p ∈ Pr | length of voyage leg p of port rotation r (nmi) |
ϕmax ∈ ℕ | maximum port service frequency (days) |
\( {q}_v^{own-m}\in \mathbb{N}\forall v\in V \) | number of vessels of type v available in company’s own fleet for deployment (vessels) |
\( {q}_v^{\mathit{\operatorname{char}}-m}\in \mathbb{N}\forall v\in V \) | number of vessels of type v available for chartering (vessels) |
ϑmax ∈ ℝ+ | maximum sailing speed (knots) |
ϑmin ∈ ℝ+ | minimum sailing speed (knots) |
Slvs ∈ ℝ+ ∀ v ∈ V, s ∈ Sv | slope of the design fuel consumption function at linear segment s for vessel type v (tons/hour) |
Invs ∈ ℝ+ ∀ v ∈ V, s ∈ Sv | intercept of the design fuel consumption function at linear segment s for vessel type v (tons/nmi) |
Bnvs ∈ ℝ+ ∀ v ∈ V, s ∈ Sv | speed reciprocal value at the beginning of linear segment s for vessel type v (knots−1) |
Edvs ∈ ℝ+ ∀ v ∈ V, s ∈ Sv | speed reciprocal value at the end of linear segment s for vessel type v (knots−1) |
\( {\alpha}_{rp}^{dem},{\beta}_{rp}^{dem}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | coefficients of the container demand sensitivity to the vessel sailing speed at port p of port rotation r |
Importrp ∈ ℝ+ ∀ r ∈ R, p ∈ Pr | portion of import containers at port p of port rotation r (%) |
\( {QC}_r^{SEA-0}\in \mathbb{N}\forall r\in R \) | total quantity of containers on board the vessel before it is moored at the first port of call under port rotation r (TEUs) |
phrpthv ∈ ℝ+ ∀ r ∈ R, p ∈ Pr, t ∈ Trp, h ∈ Hrpt, v ∈ V | handling productivity under HR h during TW t at port p of port rotation r for vessels of type v (TEUs/hour) |
AWC ∈ ℝ+ | average weight of cargo inside a standard 20-ft container (tons) |
LWTv ∈ ℝ+ ∀ v ∈ V | empty weight of a vessel of type v (tons) |
TWCv ∈ ℝ+ ∀ v ∈ V | total cargo carrying capacity of a vessel of type v (tons) |
\( {\tau}_{rp t}^{st}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r,t\in {T}_{rp} \) | start of TW t at port p of port rotation r (hours) |
\( {\tau}_{rp t}^{end}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r,t\in {T}_{rp} \) | end of TW t at port p of port rotation r (hours) |
EFSEA ∈ ℝ+ | emission factor in sea (tons of emissions/ton of fuel) |
\( {EF}_{rphv}^{PORT}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r,h\in {H}_{rpt}, \) v ∈ V | emission factor at port p of port rotation r under HR h for vessel type v (tons of emissions/TEU) |
\( {c}_v^{oper}\in {\mathbb{R}}^{+}\forall v\in V \) | unit vessel operational cost for vessel type v (USD/day) |
\( {c}_v^{char}\in {\mathbb{R}}^{+}\forall v\in V \) | unit chartering cost for vessel type v (USD/day) |
\( {c}_{rp thv}^{hand}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r,t\in {T}_{rp}, \) h ∈ Hrpt, v ∈ V | handling cost for vessel type v at port p of port rotation r during TW t under HR h (USD/TEU) |
\( {c}_{rp}^{late}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | unit late arrival cost for port p of port rotation r (USD/hour) |
cfuel ∈ ℝ+ | unit fuel cost (USD/ton) |
cinv ∈ ℝ+ | unit inventory cost (USD/TEU/hour) |
cemis ∈ ℝ+ | unit emission cost (USD/ton) |
\( {c}_{rp}^{rev}\in {\mathbb{R}}^{+}\forall r\in R,p\in {P}_r \) | unit freight rate for delivery to port p of port rotation r (USD/TEU) |
M1, M2 ∈ ℝ+ | large positive numbers |
Model formulation
HOMTLP can be further formulated as follows:
Subject to:
The objective function (23) of HOMTLP aims to maximize the total profit, estimated based on the total revenue and the total liner shipping route service cost. Constraint set (24) ensures that each port rotation will be served by only one type of vessels. Constraint set (25) guarantees that only one arrival TW will be selected at each port for each port rotation. Constraint set (26) indicates that only one vessel HR will be selected during one of the available arrival TWs for one of the vessel types at each port for each port rotation. Constraint set (27) ensures that the selected HR will be provided by the MCT operator for the selected type of vessels at each port rotation. Constraint set (28) guarantees that the selected HR will be provided by the MCT operator during the chosen arrival TW at each port for each port rotation. Constraint set (29) estimates the quantity of containers to be handled at each port of call, considering the container demand sensitivity to the vessel sailing speed. Constraints sets (30) and (31) determine the quantity of containers to be transported at each voyage leg under each port rotation. Constraints set (32) establishes the maximum quantity of containers to be transported at each voyage leg under each port rotation based on the vessel cargo carrying capacity. Constraint set (33) calculates the vessel handling time during the chosen arrival TW at each port for each port rotation.
Constraint set (34) ensures that only one segment will be selected for approximation of the fuel consumption function for each vessel type at each voyage leg of each port rotation. Constraint set (35) guarantees that the selected segment will be utilized for approximation of the fuel consumption function for the chosen vessel type at each voyage leg for each port rotation. Constraint set (36) ensures that the appropriate segment will be selected for approximation of the fuel consumption function at each voyage leg for each port rotation. Constraint set (37) computes the fuel consumption based on the selected segment at each voyage leg for each port rotation. Constraint set (38) ensures that the vessel sailing speed reciprocal is within the established limits at each voyage leg for each port rotation. Constraint set (39) calculates the sailing time at each voyage leg for each port rotation. Constraint sets (40) and (41) determine the waiting time of vessels at each port for each port rotation. Constraint set (42) estimates the late arrival time of vessels at each port for each port rotation. Constraint set (43) computes the departure time of vessels from each port for each port rotation. Constraint sets (44) and (45) calculate the arrival times of vessels at subsequent ports for each port rotation. Constraint set (46) ensures that the established port service frequency for each port rotation will be adhered to. Constraint set (47) imposes an upper bound on the port service frequency for each port rotation.
Constraint set (48) determines the total number of vessels required for each port rotation. Constraint sets (49)–(52) ensure that the required number of company’s own vessels and the required number of chartered vessels will not exceed the number of vessels available in company’s own fleet and the number of vessels available for chartering, respectively. Constraint sets (53) and (54) estimate the amount of emissions produced in sea and at ports of call for each port rotation, respectively. Constraint sets (55)–(64) compute the cost components of the HOMTLP objective function (23), including the total revenue and the total route service cost, where the total route service cost includes the total vessel operational cost, the total vessel chartering cost, the total port handling cost, the total late arrival cost, the total fuel consumption cost, the total container inventory costs in sea and at ports of call, and the total emission costs in sea and at ports of call, respectively. Constraint sets (65)–(67) define the nature of different decision variables, auxiliary variables, as well as parameters of HOMTLP.
Solution approach
HOMTLP is a mixed-integer nonlinear programming model, which can be solved to the global optimality using exact optimization algorithms. A number of commercial mixed-integer nonlinear programming solvers are available on the market, such as BARON, BONMIN, COUENNE, LINDO, SCIP, and others. In this study, BARON (Branch-and-Reduce Optimization Navigator) will be employed as the solution approach. BARON is an advanced system that is used to solve nonlinear and mixed-integer nonlinear nonconvex optimization problems to the global optimality. It is available under several modeling languages, such as AIMMS, AMPL, GAMS, etc. Based on the advanced branch-and-bound concepts, BARON applies certain algorithms that rely on interval analysis, constraint propagation, and duality techniques in order to reduce ranges of the considered variables (GAMS, 2019). Furthermore, BARON constructs rigorous relaxations by means of enlarging the feasible space for a given optimization problem of interest. All the nonlinear variables and expressions in the mathematical program must be assigned upper and lower bounds by the user before executing BARON.
Computational experiments and managerial insights
This section of the manuscript presents some computational experiments that were conducted to showcase the HOMTLP’s potential to assist liner shipping companies with an integrated decision making at the tactical level. Moreover, certain important managerial insights, which were drawn from the computational experiments, are exhibited in this section as well. Throughout this study, the computational experiments were conducted on a Dell Alienware Intel(R) Core™ i7-7700K processor with 32 GB of RAM and Windows 10 Operating System. MATLAB 2016a was used to generate the piecewise secant approximations for the fuel consumption function. HOMTLP was encoded in the GAMS (General Algebraic Modeling System) environment and then solved to the global optimality with BARON (GAMS, 2019). The maximum runtime for BARON was set to 15 min, while the maximum optimality gap was restricted to 3%. An additional analysis was performed to assess the efficiency of the adopted solution approach, and details are presented in section 5.2 of the manuscript.
Input data description
A total of three Asia-North America liner shipping routes, served by Compagnie Maritime d’Affrètement Compagnie Générale Maritime (CMA CGM), were considered to demonstrate the performance of the developed methodology. The routes and the associated ports of call are illustrated in Fig. 3 (CMA CGM, 2019a). The distances between consecutive ports (lrp, r ∈ R, p ∈ Pr – nmi), which were obtained from SEA-DISTANCES.ORG (2019), are denoted in parentheses (see Fig. 3). Table 1 presents the numerical data that were required to conduct the computational experiments. The numerical data were obtained from the liner shipping and freight terminal operations literature (Wang and Meng, 2012a-c; Psaraftis and Kontovas, 2013; Wang et al., 2014; Dulebenets et al., 2018; Abioye et al., 2019; Cheaitou and Cariou, 2019; CMA, 2019a,b; Kavoosi et al., 2019a,b; Theophilus et al., 2019). Two types of vessels were selected for the computational experiments (i.e., n3 = 2). However, each port rotation could be served by only one type of vessels. The liner shipping company was offered three arrival TWs at each port of call (i.e., \( {n}_{rp}^4=3\forall r\in R,p\in {P}_r \)). Under each arrival TW, four HRs were available at each port of call (i.e., \( {n}_{rp t}^5=4\forall r\in R,p\in {P}_r,t\in {T}_{rp} \)).
The port service frequency in HOMTLP is a variable. However, its upper bound was set to 14 days (i.e., bi-weekly frequency). The number of vessels of type v available in the company’s own fleet (\( {q}_v^{own-m},v\in V \)) and the number of vessels of type v available for chartering (\( {q}_v^{\mathit{\operatorname{char}}-m},v\in V \)) varied from 3 to 6 vessels. The vessel sailing speed was restricted to vary within 15 knots and 25 knots (Wang and Meng, 2012a,b). The container demand at each port of call (\( {\boldsymbol{QC}}_{rp}^{PORT},r\in R,p\in {P}_r \)) was assumed to be within the range of 200 TEUs to 2000 TEUs (Dulebenets, 2018a; Abioye et al., 2019). The coefficients of container demand (\( {\alpha}_{rp}^{dem} \), \( {\beta}_{rp}^{dem},r\in R,p\in {P}_r \)) were set as U[400; 1,800] TEUs and U[1,250; 3,000] TEUs, respectively, where U denotes uniformly distributed pseudorandom numbers with the lower and upper bounds, presented in square brackets. Note that container demand includes both export container demand and import container demand. The portion of import containers at each port (Importrp, r ∈ R, p ∈ Pr) was set to uniformly vary within 40% and 60%, whereas the portion of export containers was set as (1 − Importrp) ∀ r ∈ R, p ∈ Pr.
The total quantity of containers on board each vessel before mooring at the first port of call under port rotation r (i.e., payload at the last voyage leg) was set as follows: \( {QC}_r^{SEA-0}=U\left[\mathrm{4,000};\mathrm{7,000}\right]\forall r\in R \) (TEUs). The handling productivity under HR h during TW t at port p of port rotation r for vessels of type v (phrpthv, r ∈ R, p ∈ Pr, t ∈ Trp, h ∈ Hrpt, v ∈ V) was set to U[50; 125] TEUs/hour. Based on the operational data, reported by the CMA CGM liner shipping company (CMA CGM, 2019b), the average weight of cargo inside a standard 20-ft container (AWC) was assumed to be 11 tons. The empty weight of a vessel of type v (LWTv, v ∈ V) varied from 48,000 tons to 50,000 tons, while the total cargo carrying capacity of a vessel of type v (TWCv, v ∈ V) was assumed to range from 144,000 tons to 150,000 tons (CMA CGM, 2019b). The start of TW t at port p + 1 under port rotation r was estimated based on the relationship between the start of TW t at port p under port rotation r, length of voyage leg p under port rotation r, and the vessel sailing speed bounds as follows: \( {\tau}_{r\left(p+1\right)t}^{st}={\tau}_{rp t}^{st}+\frac{l_{rp}}{U\left[{\vartheta}^{min};{\vartheta}^{max}\right]}\forall r\in R,p\in {P}_r,t\in {T}_{rp} \) (hours) (Dulebenets, 2018a; Abioye et al., 2019).
Moreover, the arrival TW duration at each port under each port rotation was restricted to U[12; 24] hours. Emissions of carbon dioxide by the main vessel engines were modeled throughout the computational experiments. The emission factor in sea (EFSEA) was assumed to be 3.082 tons of carbon dioxide per ton of fuel (Psaraftis and Kontovas, 2013; Kontovas, 2014). On the other hand, the emission factor at ports was set to 0.01729 tons of carbon dioxide per TEU for the baseline handling productivity of 180 TEUs/hour (Tran et al., 2017). For the handling productivities other than the baseline handling productivity, the emission factor at ports was estimated as follows: \( {EF}_{rp hv}^{PORT}=0.01729+U\left[1.0;1.2\right]\bullet \frac{\left[\left(\sum \limits_{t\in {T}_{rp}}{ph}_{rp t hv}/{n}_{rp}^4\right)-180\right]}{180}\bullet 0.01729\forall r\in R,p\in {P}_r,h\in {H}_{rp t},v\in V \) (tons of carbon dioxide per TEU) (Dulebenets, 2018a).
The unit vessel operational cost (\( {c}_v^{oper},v\in V \)) was restricted to vary between 39,000 USD/day and 43,000 USD/day, whereas the unit vessel chartering cost (\( {c}_v^{char},v\in V \)) was assumed to be within 59,000 USD/day and 65,000 USD/day. The unit handling cost for vessel type v at port p of port rotation r during TW t under HR h was estimated as follows: \( {c}_{rp t hv}^{hand}=U\left[200;500\right]\forall r\in R,p\in {P}_r,t\in {T}_{rp},h\in {H}_{rp t},v\in V \) (USD/TEU). The unit late arrival cost at ports (\( {c}_{rp}^{late},r\in R,p\in {P}_r \)) was set to U[5,000; 8,000] USD/hour (Dulebenets, 2018a-b; Abioye et al., 2019). The unit fuel cost (cfuel) was assumed to be 200 USD/ton (Wang and Meng, 2012a,b). The unit inventory cost was set to cinv = 0.25 USD/TEU/hour. The unit emission cost (cemis) was set to 32 USD/ton (Tran et al., 2017). Furthermore, the unit freight rate was set to \( {c}_{rp}^{rev}=U\left[\mathrm{1,000};\mathrm{2,500}\right]\forall r\in R,p\in {P}_r \) (USD/TEU).
Performance of the adopted solution approach
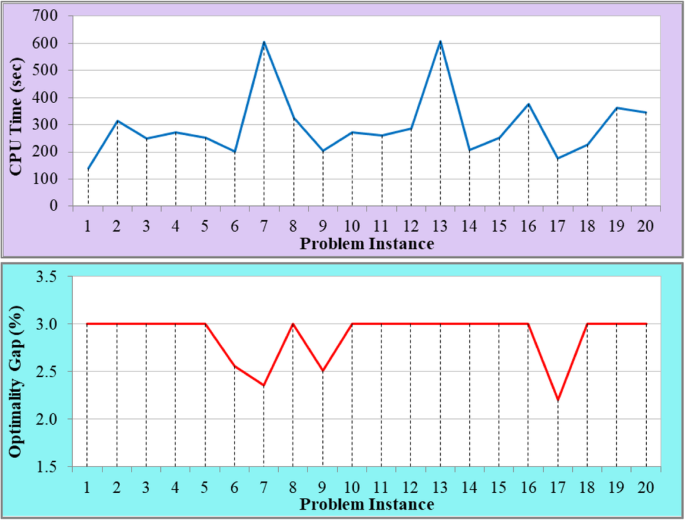
As mentioned earlier, BARON was selected as a solution approach for HOMTLP. In order to assess the performance of the adopted solution approach, a total of 20 problem instances were generated by changing the start and end of arrival TWs at ports of call under each one of the considered port rotations. The procedure to randomly generate the start and end of arrival TWs is discussed in section 5.1 of the manuscript. For each problem instance, the maximum runtime for BARON was set to 15 min, while the maximum optimality gap was restricted to 3%. The number of variables and the number of constraints for every problem instance were also recorded. For each problem instance, HOMTLP included 1853 variables and 3063 constraints. Note that the number of linear segments in the piecewise approximation for the design fuel consumption function was set to 10 linear segments based on the preliminary computational experiments. The piecewise approximation with 10 linear segments demonstrated a high degree of accuracy (see Fig. 2) without substantially impacting the computational time, required by BARON to solve HOMTLP.
Figure 4 presents the computational performance of the adopted solution approach, including the CPU time and optimality gap values for each problem instance. The CPU times for the problem instances ranged between 140.54 s (problem instance #1) and 608.54 s (problem instance #13). Moreover, the CPU time was less than 400 s for 18 out the 20 considered problem instances. As for the optimality gaps, the solutions, returned by BARON, had the optimality gaps between 2.2% and 3% for the 20 problem instances. Note that the optimality gap values could be reduced by increasing the runtime for BARON. For example, problem instances #1 and #2 both had an optimality gap of 3%. However, the CPU time for problem instance #1 (140.54 s) was significantly lower than the CPU time for problem instance #2 (315.82 s). If the maximum optimality gap restriction of 3% was relaxed, and BARON was allowed to run for 315.82 s (i.e., the CPU time recorded for problem instance #2); then, a better optimality gap could be achieved for problem instance #1 as compared to problem instance #2. Based on the conducted analysis, it can be concluded that BARON was able to obtain good-quality solutions for HOMTLP within a reasonable computational time.
Managerial insights
This section of the manuscript outlines important managerial insights, which were obtained from the tactical-level decisions that were suggested by HOMTLP. In particular, the managerial insights were retrieved via a set of sensitivity analyses of the tactical-level decisions, which were suggested by HOMTLP, to the following aspects: (1) port arrival TW availability; (2) port HR availability; (3) unit fuel cost; (4) unit emission cost; and (5) unit operational and chartering costs. The conducted sensitivity analyses are further described in the following sections of the manuscript.
Sensitivity of the tactical-level decisions to the port arrival TW availability
A total of 4 scenarios were developed by changing the arrival TW availability at ports in order to conduct a sensitivity analysis of the tactical-level decisions. TWs “1”, “2”, and “3” were suggested to the liner shipping company at each port for the TW availability scenarios #1, #2, and #3, respectively. On the contrary, all 3 considered TWs were available in the TW availability scenario #4. The remaining parameter values of HOMTLP (see Table 1) were unchanged for all the TW availability scenarios. Figure 5 presents the results of the sensitivity analysis for the port arrival TW availability, which include the sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, average port handling productivity, and total profit. Note that the average vessel sailing speed (AvgWtSS) was weighted by voyage leg length \( \left( AvgWtSS=\frac{\sum \limits_{r\in R}\sum \limits_{p\in {P}_r}{\boldsymbol{\vartheta}}_{rp}{l}_{rp}}{\sum \limits_{r\in R}\sum \limits_{p\in {P}_r}{l}_{rp}}\right) \) and the average port handling productivity (AvgWtHP) was weighted by container demand \( \left( AvgWtHP=\frac{\sum \limits_{r\in R}\sum \limits_{p\in {P}_r}\sum \limits_{t\in {T}_{rp}}\sum \limits_{h\in {H}_{rp t}}\sum \limits_{v\in V}{ph}_{rp t hv}{\boldsymbol{QC}}_{rp}^{PORT}{\boldsymbol{x}}_{rp t hv}}{\sum \limits_{r\in R}\sum \limits_{p\in {P}_r}{\boldsymbol{QC}}_{rp}^{PORT}}\right) \) in order to capture the effects of voyage leg length and container demand at ports, respectively.
The sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, average port handling productivity, and total profit to the port arrival TW availability. Shows changes in the average vessel sailing speed, average port service frequency, total vessels deployed, average port handling productivity, and total profit for different TW availability scenarios
As suggested by Fig. 5, the average vessel sailing speed was the highest in scenario #1 (23.76 knots), while the lowest average vessel sailing speed was recorded in scenario #2 (22.81 knots). On the other hand, the lowest and highest average port service frequencies were observed for scenarios #4 and #3, respectively (13 days and 10 days, respectively). Note that the lowest port service frequency corresponds to the largest number of days between consecutive visits of a given port. It was also found that the liner shipping company was required to deploy the largest number of vessels to serve the considered port rotations in scenario #3 and guarantee the selected port service frequency for each port rotation. Such a finding can be explicated by the fact that the ports of call had to be served more frequently in scenario #3 as compared to the other port arrival TW availability scenarios. Scenarios #1 and #4 on the contrary had lower average port service frequencies and, hence, required the smallest number of vessels (8 vessels). The computational experiments show that the average port handling productivity was the highest in scenario #2 (103.35 TEUs/hour), while the lowest port handling productivity was recorded in scenario #3 (91.72 TEUs/hour). Moreover, it was found that the highest profit (24,052,953 USD) was recorded in scenario #4, where all the arrival TWs were available. Therefore, availability of multiple port arrival TWs provided more flexibility to the liner shipping company in terms of setting the appropriate values for the key decision variables (i.e., vessel sailing speeds, port service frequencies, total number of vessels deployed, HRs at ports call) and allowed improving the overall efficiency of liner shipping operations.
Sensitivity of the tactical-level decisions to the port HR availability
A total of 5 scenarios were developed by changing the port HR availability in order to conduct a sensitivity analysis of the tactical-level decisions. HRs “1”, “2”, “3”, and “4” were offered by the MCT operators to the liner shipping company at each port of call for the HR availability scenarios #1, #2, #3, and #4, respectively. On the contrary, all 4 considered HRs were available in the HR availability scenario #5. The remaining parameter values of HOMTLP (see Table 1) were unchanged for all the HR availability scenarios. Figure 6 presents the results of the sensitivity analysis for the port HR availability, which include the sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, average port handling productivity, and total profit.
The sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, average port handling productivity, and total profit to the port HR availability. Shows changes in the average vessel sailing speed, average port service frequency, total vessels deployed, average port handling productivity, and total profit for different HR availability scenarios
As suggested by Fig. 6, the average vessel sailing speed was the highest in scenario #2 (23.73 knots), while the lowest average vessel sailing speed was recorded in scenario #5 (23.51 knots). The highest average port service frequency was observed in scenario #2 (9.67 days), and, therefore, this scenario required the largest number of vessels to be deployed (11 vessels). The other port HR availability scenarios on the contrary had lower average port service frequencies and, hence, required fewer vessels to serve the considered port rotations (8 vessels). The computational experiments show that the average port handling productivity was the highest in scenario #4 (97.38 TEUs/hour), while the lowest port handling productivity was recorded in scenario #2 (83.87 TEUs/hour). Moreover, it was found that the highest profit (24,052,953 USD) was recorded in scenario #5, where all the port HRs were available. Therefore, availability of multiple port HRs provided more flexibility to the liner shipping company in terms of setting the appropriate values for the key decision variables (i.e., vessel sailing speeds, port service frequencies, total number of vessels deployed, HRs at ports call) and allowed improving the overall efficiency of liner shipping operations.
Sensitivity of the tactical-level decisions to the unit fuel cost
A total of 12 unit fuel cost scenarios were developed by increasing the unit fuel cost from 200 USD/ton in scenario #1 to 750 USD/ton in scenario #12 (an increment of 50 USD/ton was used). The remaining parameter values of HOMTLP (see Table 1) were unchanged for all the unit fuel cost scenarios. Figure 7 presents the results of the unit fuel cost sensitivity analysis, which include the sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity. Since the unit fuel cost was increased, the solution approach (i.e., BARON) attempted to mitigate the impact on the total fuel cost by reducing the average vessel sailing speed (i.e., average vessel sailing speed decreased by 9.11% from scenario #1 to scenario #12). Moreover, increments in the unit fuel cost from one scenario to another caused an increase in the average port service frequency. The total number of vessels to be deployed increased due to an increase in the average port service frequency. On the other hand, the average handling productivity remained almost the same. The sensitivity of the average container demand at ports to the unit fuel cost is demonstrated in Fig. 8, where it can be observed that the container demand reduced when the unit fuel cost was increased. The latter pattern can be explicated by the fact that the container demand at ports is a function of the vessel sailing speed. Since the average vessel sailing speed decreased due to increments in the unit fuel cost, the container demand decreased as well. Furthermore, the total profit in scenario #12 was 22.19% lower than the total profit in scenario #1 due to an increase in the unit fuel cost.
The sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity to the unit fuel cost. Shows changes in the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity for different unit fuel cost scenarios
Sensitivity of the tactical-level decisions to the unit emission cost
A total of 20 unit emission cost scenarios were developed by increasing the unit emission cost from 16 USD/ton in scenario #1 to 320 USD/ton in scenario #20 (an increment of 16 USD/ton was used). The remaining parameter values of HOMTLP (see Table 1) were unchanged for all the unit emission cost scenarios. Figure 9 presents the results of the unit emission cost sensitivity analysis, which include the sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity.
The sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity to the unit emission cost. Shows changes in the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity for different unit emission cost scenarios
In order to mitigate the effect of increments in the unit emission cost on the total profit and to reduce emissions in sea, the solution approach reduced the average vessel sailing speed by 14.59% from scenario #1 to scenario #20. Due to an increase in the unit emission cost, the average port service frequency experienced an increasing pattern, which triggered an increase in the total number of vessels required for deployment. Furthermore, as the unit emission cost was increased from one scenario to another, the average port handling productivity increased. An increase in the average port handling productivity can be justified by the fact that the liner shipping company aimed to decrease the vessel handling time at ports and use these time savings to compensate for the time losses in sea (due to a reduction in the average vessel sailing speed). The sensitivity of the total amount of emissions produced in sea to the unit emission cost is demonstrated in Fig. 10, where it can be observed that the total amount of emissions produced in sea reduced when the unit emission cost was increased. Such a reduction can be explicated by the fact that the amount of emissions produced in sea is proportional to the total fuel consumption at voyage legs and, thereby, to the vessel sailing speed, which decreased after increasing the unit emission cost. Furthermore, the total profit in scenario #20 was 35.61% lower than the total profit in scenario #1 due to an increase in the unit emission cost.
Sensitivity of the tactical-level decisions to the unit operational and chartering costs
A sensitivity analysis for the unit operational and chartering costs was carried out by developing 20 scenarios and increasing the unit operational and chartering costs from one scenario to another. The unit operational cost for vessel type “1” was increased from 10,000 USD/day in scenario #1 to 200,000 USD/day in scenario #20 (an increment of 10,000 USD/day was used), while the unit operational cost for vessel type “2” was increased from 9000 USD/day in scenario #1 to 180,000 USD/day in scenario #20 (an increment of 9000 USD/day was used). In a similar fashion, the unit chartering cost for vessel type “1” was increased from 15,000 USD/day in scenario #1 to 300,000 USD/day in scenario #20 (an increment of 15,000 USD/day was used), while the unit chartering cost for vessel type “2” was increased from 13,500 USD/day in scenario #1 to 270,000 USD/day in scenario #20 (an increment of 13,500 USD/day was used). The remaining parameter values of HOMTLP (see Table 1) were unchanged for all the unit operational/chartering cost scenarios.
Figure 11 presents the results of the sensitivity analysis for the unit operational and chartering costs, which include the sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity. As the unit operational and chartering costs were increased, the solution approach increased the average vessel sailing speed by 7.05% from scenario #1 to scenario #20. In order to mitigate the effect of increments in the unit operational and chartering costs on the total profit, the total number of vessels to be deployed reduced from one scenario to another. The computational experiments show that no vessels were chartered for 12 scenarios out of the 20 developed scenarios after increasing the unit chartering cost. As the number of deployed vessels decreased from one scenario to another, the average port service frequency generally experienced a decreasing pattern (i.e., the ports of call were served less frequently). On the other hand, the average handling productivity remained almost the same. Furthermore, the total profit in scenario #20 was 65.49% lower than the total profit in scenario #1 due to an increase in the unit operational and chartering costs.
The sensitivity of the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity to the unit operational and chartering costs. Shows changes in the average vessel sailing speed, average port service frequency, total vessels deployed, and average port handling productivity for different unit operational/chartering cost scenarios
Concluding remarks
Liner shipping companies spend thousands of dollars every day in vessel operational costs, fuel costs, port handling costs, and other route service costs. In order to solidify their position in a highly competitive industry, liner shipping companies are required to effectively address strategic, tactical, and operational decision problems. This study focused on the tactical-level decision problems in liner shipping, including port service frequency determination, fleet deployment, sailing speed optimization, and vessel schedule design. A significant portion of the published studies addressed each tactical-level decision problem separately. Certain studies incorporated multiple tactical-level decision problems; however, none of them addressed all the four decision problems simultaneously. Decisions, provided by separate solution approaches for separate decision problems, may not be compatible with each other. Moreover, liner shipping companies seek integrated solution methodologies that can tackle multiple decision problems simultaneously for a given planning horizon. This study proposed a novel holistic optimization model for tactical-level planning in liner shipping (HOMTLP), which captures all the tactical-level decision problems, including port service frequency determination, fleet deployment, sailing speed optimization, and vessel schedule design.
The objective of HOMTLP was to maximize the total profit from the cargo shipment, estimated based on the total revenue generated and the total route service cost incurred. The key route service cost components, found in the liner shipping literature, were considered. The proposed HOMTLP captured important features of liner shipping operations. First, the fuel consumption by the main vessel engines was estimated not only based on the vessel sailing speed (which is a common approach in the existing liner shipping literature) but also based on the vessel payload. Second, the container demand at ports was assumed to be elastic and decreased with increasing transit time of containers. Third, HOMTLP assumed that multiple time windows and handling rates were offered to serve the vessels at each port of call in order to improve the efficiency of liner shipping operations and improve the utilization of the available handling equipment at marine container terminals. Fourth, the container inventory costs in sea and at ports were directly accounted for throughout the tactical-level planning by HOMTLP. Fifth, HOMTLP directly captured the quantity of emissions that are produced by vessels in sea and from container handling at ports, which will further allow enhancing the environmental sustainability of the international trade and liner shipping operations.
A set of linearization strategies were applied in order to reduce the degree of the model’s nonlinearity. An exact optimization approach (BARON) was adopted to solve HOMTLP. The computational experiments were conducted using the operational data, collected for the liner shipping routes served by the CMA CGM liner shipping company. A number of sensitivity analyses were conducted to showcase some important managerial insights using the proposed methodology. Potential future research extensions for this study include, but are not limited to, the following: (a) model various sources of uncertainty in liner shipping (e.g., uncertainties in shipment demand, port times, sailing times); (b) evaluate various vessel schedule recovery options to compensate for the delays caused by uncertainties in liner shipping (e.g., vessel sailing speed adjustment, port skipping, port swapping); (c) consider heterogeneity of the vessel fleet serving a given port rotation (i.e., different vessel types are allowed to serve a given port rotation); (d) develop game-theoretic models for negotiation of arrival time windows and handling rates at ports of call; and (e) develop heuristic algorithms that can provide good-quality solutions for HOMTLP within a reasonable computational time.
Availability of data and materials
The data, which were used throughout the numerical experiments, can be obtained from the corresponding author upon request.
Abbreviations
- BARON:
-
Branch-and-Reduce Optimization Navigator
- CMA CGM:
-
Compagnie Maritime d’Affrètement Compagnie Générale Maritime
- ECA:
-
Emission Control Area
- GAMS:
-
General Algebraic Modeling System
- HOMTLP:
-
Holistic Optimization Model for Tactical-Level Planning in Liner Shipping
- HR:
-
Handling Rate
- IMO:
-
International Maritime Organization
- MCT:
-
Marine Container Terminal
- nmi:
-
Nautical Miles
- TEU:
-
Twenty-Foot Equivalent Unit
- TW:
-
Time Window
- USD:
-
United States Dollars
References
Abioye OF, Dulebenets MA, Pasha J, Kavoosi M (2019) A vessel schedule recovery problem at the liner shipping route with emission control areas. Energies 12(12):2380
Achurra-Gonzalez PE, Angeloudis P, Goldbeck N, Graham DJ, Zavitsas K, Stettler ME (2019) Evaluation of port disruption impacts in the global liner shipping network. J Shipping Trade 4(1):3
Adland, R.O. and Jia, H., 2016. Vessel speed analytics using satellite-based ship position data. Paper presented at the 2016 IEEE international conference on industrial engineering and engineering management (IEEM). Accessed on 08.27.2019 from https://ieeexplore.ieee.org/document/7798088
Alharbi A, Wang S, Davy P (2015) Schedule design for sustainable container supply chain networks with port time windows. Adv Eng Inform 29:322–331
Álvarez JF (2009) Joint routing and deployment of a fleet of container vessels. Marit Econ Logistics 11(2):186–208
Aydin N, Lee H, Mansouri SA (2017) Speed optimization and bunkering in liner shipping in the presence of uncertain service times and time windows at ports. Eur J Oper Res 259(1):143–154
Bendall HB, Stent AF (2001) A scheduling model for a high speed containership service: a hub and spoke short-sea application. Int J Marit Econ 3(3):262–277
Cheaitou A, Cariou P (2012) Liner shipping service optimization with reefer containers capacity: an application to northern Europe–South America trade. Marit Policy Manag 39(6):589–602
Cheaitou A, Cariou P (2019) Greening of maritime transportation: a multi-objective optimization approach. Ann Oper Res 273(1–2):501–525
Chen Z, Lei L, Zhong H (2007) Container vessel scheduling with bi-directional flows. Oper Res Lett 35(2):186–194
CMA CGM, 2019a. Line services. Accessed on 08.27.2019 from https://www.cma-cgm.com/products-services/line-services/solution
CMA CGM, 2019b. Bohai. Accessed on 08.27.2019 from https://www.cma-cgm.com/products-services/line-services/flyer/BOHAI
De A, Mamanduru VKR, Gunasekaran A, Subramanian N, Tiwari MK (2016) Composite particle algorithm for sustainable integrated dynamic ship routing and scheduling optimization. Comput Ind Eng 96:201–215
Dulebenets MA (2018a) A comprehensive multi-objective optimization model for the vessel scheduling problem in liner shipping. Int J Prod Econ 196:293–318
Dulebenets MA (2018b) The vessel scheduling problem in a liner shipping route with heterogeneous fleet. Int J Civil Eng 16:1–32
Dulebenets MA (2018c) Green vessel scheduling in liner shipping: modeling carbon dioxide emission costs in sea and at ports of call. Int J Transport Sci Technol 7(1):26–44
Dulebenets MA (2018d) The green vessel scheduling problem with transit time requirements in a liner shipping route with emission control areas. Alexandria Eng Journal 57(1):331–342
Dulebenets MA (2019) Minimizing the total liner shipping route service costs via application of an efficient collaborative agreement. IEEE Trans Intell Transp Syst 20(1):123–136
Dulebenets MA, Kavoosi M, Abioye OF, Pasha J (2018) A self-adaptive evolutionary algorithm for the berth scheduling problem: towards efficient parameter control. Algorithms 11(7):100
Dulebenets MA, Ozguven EE (2017) Vessel scheduling in liner shipping: modeling transport of perishable assets. Int J Prod Econ 184:141–156
Dulebenets MA, Pasha J, Abioye OF, Kavoosi M (2019) Vessel scheduling in liner shipping: a critical literature review and future research needs. Flexible Serv Manuf J. https://doi.org/10.1007/s10696-019-09367-2 – in press
Fagerholt K (2001) Ship scheduling with soft time windows: an optimisation based approach. Eur J Oper Res 131(3):559–571
Fagerholt K, Laporte G, Norstad I (2010) Reducing fuel emissions by optimizing speed on shipping routes. J Oper Res Soc 61(3):523–529
Fagerholt K, Psaraftis HN (2015) On two speed optimization problems for ships that sail in and out of emission control areas. Transp Res Part D: Transp Environ 39:56–64
Fugazza M, Hoffmann J (2017) Liner shipping connectivity as determinant of trade. J Shipping Trade 2(1):1
GAMS, 2019. GAMS – BARON. Accessed on 08.27.2019 from https://www.gams.com/latest/docs/S_BARON.html/
Gelareh S, Maculan N, Mahey P, Monemi RN (2013) Hub-and-spoke network design and fleet deployment for string planning of liner shipping. Appl Math Model 37(5):3307–3321
Gelareh S, Pisinger D (2011) Fleet deployment, network design and hub location of liner shipping companies. Transportation Res E 47(6):947–964
Giovannini M, Psaraftis HN (2019) The profit maximizing liner shipping problem with flexible frequencies: logistical and environmental considerations. Flex Serv Manuf J 31:567–597
Gürel S, Shadmand A (2019) A heterogeneous fleet liner ship scheduling problem with port time uncertainty. CEJOR 27(4):1153–1175
Hoffmann J, Wilmsmeier G, Lun YV (2017) Connecting the world through global shipping networks. J Shipping Trade 2(1):2
Hsu C, Hsieh Y (2007) Routing, ship size, and sailing frequency decision-making for a maritime hub-and-spoke container network. Math Comput Model 45(7–8):899–916
Huang Y, Hu J, Yang B (2015) Liner services network design and fleet deployment with empty container repositioning. Comput Ind Eng 89:116–124
Kavirathna C, Kawasaki T, Hanaoka S, Matsuda T (2018) Transshipment hub port selection criteria by shipping lines: the case of hub ports around the bay of Bengal. J Shipping Trade 3(1):4
Kavoosi M, Dulebenets MA, Abioye O, Pasha J, Theophilus O, Wang H, Kampmann R, Mikijeljević M (2019b) Berth scheduling at marine container terminals: a universal island-based metaheuristic approach. Maritime Business Review. https://doi.org/10.1108/MABR-08-2019-0032 – in press
Kavoosi M, Dulebenets MA, Abioye OF, Pasha J, Wang H, Chi H (2019a) An augmented self-adaptive parameter control in evolutionary computation: a case study for the berth scheduling problem. Adv Eng Inform 42:100972
Kontovas CA (2014) The green ship routing and scheduling problem (GSRSP): a conceptual approach. Transp Res Part D: Transp Environ 31:61–69
Lin D, Tsai Y (2014) The ship routing and freight assignment problem for daily frequency operation of maritime liner shipping. Transport Res E 67:52–70
Liu Z, Wang S, Du Y, Wang H (2016) Supply chain cost minimization by collaboration between liner shipping companies and port operators. Transp J 55(3):296–314
MAN Diesel & Turbo, 2012. Basic Principle of Ship Propulsion. Accessed on 08.27.2019 from https://spain.mandieselturbo.com/docs/librariesprovider10/sistemas-propulsivos-marinos/basic-principles-of-ship-propulsion.pdf?sfvrsn=2
Meng Q, Wang S (2011) Optimal operating strategy for a long-haul liner service route. Eur J Oper Res 215(1):105–114
Meng Q, Wang S, Andersson H, Thun K (2014) Containership routing and scheduling in liner shipping: overview and future research directions. Transp Sci 48(2):159–312
Ng M (2015) Container vessel fleet deployment for liner shipping with stochastic dependencies in shipping demand. Transp Res B Methodol 74:79–87
Ng M, Lin D (2018) Fleet deployment in liner shipping with incomplete demand information. Transport Res E 116:184–189
Pesenti R (1995) Hierarchical resource planning for shipping companies. Eur J Oper Res 86:91–102
Psaraftis HN, Kontovas CA (2013) Speed models for energy-efficient maritime transportation: a taxonomy and survey. Transport Res C 26:331–351
Ronen D (2011) The effect of oil price on containership speed and fleet size. J Oper Res Soc 62:211–216
SEA-DISTANCES.ORG, 2019. Accessed on 08.27.2019 from https://sea-distances.org/
Sheng X, Chew EP, Lee LH (2015) (s, S) policy model for liner shipping refueling and sailing speed optimization problem. Transport Res E 76:76–92
Song D, Li D, Drake P (2015) Multi-objective optimization for planning liner shipping service with uncertain port times. Transport Res E 84:1–22
Tan Z, Wang Y, Meng Q, Liu Z (2018) Joint ship schedule design and sailing speed optimization for a single inland shipping service with uncertain dam transit time. Transp Sci 52(6):1570–1588
Theophilus O, Dulebenets MA, Pasha J, Abioye OF, Kavoosi M (2019) Truck scheduling at cross-docking terminals: a follow-up state-of-the-art review. Sustainability 11(19):5245
Tran NK, Haasis H, Buer T (2017) Container shipping route design incorporating the costs of shipping, inland/feeder transport, inventory and CO2 emission. Marit Econ Logistics 19:667–694
UNCTAD, 2018. Review of maritime transport 2018. United Nations Conference on Trade and Development
Wang S, Alharbi A, Davy P (2014) Liner ship route schedule design with port time windows. Transport Res C 41:1–17
Wang S, Meng Q (2012a) Sailing speed optimization for container ships in a liner shipping network. Transport Res E 48(3):701–714
Wang S, Meng Q (2012b) Robust schedule design for liner shipping services. Transport Res E 48(6):1093–1106
Wang S, Meng Q (2012c) Liner ship route schedule design with sea contingency time and port time uncertainty. Transp Res B Methodol 46(5):615–633
Wang S, Meng Q (2015) Robust bunker management for liner shipping networks. Eur J Oper Res 243:789–797
Wang S, Meng Q (2017) Container liner fleet deployment: a systematic overview. Transport Res C 77:389–404
Wang S, Meng Q, Liu Z (2013) Bunker consumption optimization methods in shipping: a critical review and extensions. Transport Res C 53:49–62
Wang S, Wang X (2016) A polynomial-time algorithm for sailing speed optimization with containership resource sharing. Transp Res B Methodol 93(A):394–405
Wang X, Fagerholt K, Wallace SW (2018a) Planning for charters: a stochastic maritime fleet composition and deployment problem. Omega 79:54–66
Wang Y, Meng Q, Kuang H (2018b) Jointly optimizing ship sailing speed and bunker purchase in liner shipping with distribution-free stochastic bunker prices. Transport Res C 89:35–52
Wang Y, Meng Q, Kuang H (2019) Intercontinental liner shipping service design. Transp Sci 53(2):344–364
Wong EYC, Tai AH, Lau HYK, Raman M (2015) An utility-based decision support sustainability model in slow steaming maritime operations. Transport Res E 78:57–69
Yao Z, Ng SH, Lee LH (2012) A study on bunker fuel management for the shipping liner services. Comput Oper Res 39(5):1160–1172
Zhang A, Lam JSL (2014) Impacts of schedule reliability and sailing frequency on the liner shipping and port industry: a study of daily Maersk. Transp J 53(2):235–253
Zhao Y, Jia R, Jin N, He Y (2016) A novel method of fleet deployment based on route risk evaluation. Inf Sci 372:731–744
Zhen L, Hu Y, Wang S, Laporte G, Wu Y (2019a) Fleet deployment and demand fulfillment for container shipping liners. Transp Res B Methodol 120:15–32
Zhen L, Shen T, Wang S, Yu S (2016) Models on ship scheduling in transshipment hubs with considering bunker cost. Int J Prod Econ 173:111–121
Zhen L, Wang S, Laporte G, Hu Y (2019b) Integrated planning of ship deployment, service schedule and container routing. Comput Oper Res 104:304–318
Acknowledgments
Not applicable.
Funding
This work has been partially supported by the National Science Foundation grant CMMI-1901109 and the China Merchants Energy Shipping. The opinions, findings, and conclusions, expressed in this publication, are those of the authors and do not necessarily reflect the views of the National Science Foundation and the China Merchants Energy Shipping.
Author information
Authors and Affiliations
Contributions
The authors confirm contributions to the paper as follows: J.P. and M.A.D. were responsible for the study conception and design; J.P., M.K., O.F.A., and O.T. were responsible for data collection; J.P. and M.A.D. were responsible for analysis and interpretation of the results; J.P., M.A.D., H.W., R.K., and W.G. were responsible for the draft manuscript preparation. All authors reviewed the results and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pasha, J., Dulebenets, M.A., Kavoosi, M. et al. Holistic tactical-level planning in liner shipping: an exact optimization approach. J. shipp. trd. 5, 8 (2020). https://doi.org/10.1186/s41072-020-00060-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41072-020-00060-4